Executive Summary:
Sparse logistic regression plays a central role in scientific and industrial applications where both predictive accuracy and interpretability are required. However, enforcing exact sparsity through an ℓ₀ constraint leads to a challenging combinatorial optimization problem. Branch and bound frameworks provide a principled way to obtain globally optimal sparse models, but their performance is fundamentally limited by repeated subproblem solves and by the size of the search tree.
This project develops new algorithms and computational techniques to improve the scalability of branch and bound for ℓ₀-constrained logistic regression. We introduce two major advancements: (1) a parallel branch and bound architecture that distributes branching decisions across multiple worker processes, and (2) a GPU-accelerated stochastic gradient descent solver tailored for the subproblems encountered during search. Together, these enhancements substantially reduce runtime while preserving solution quality.
Our experiments demonstrate that parallel branching achieves near-ideal speedup up to four workers, and that GPU-accelerated stochastic gradient descent provides more than an order-of-magnitude improvement over CPU-based subsolvers. Furthermore, despite the nonconvex landscape, the GPU-based subsolver maintains high accuracy in lower-bound estimation, enabling effective pruning of the search tree.
Overall, this work shows that principled algorithm design—combined with modern parallel and GPU computing—can dramatically accelerate exact sparse logistic regression, making global feature selection more feasible at scale.
Research Motivation:
Logistic regression is one of the most widely used statistical models for binary classification across science, engineering, medicine, and finance. Its appeal stems from its interpretability and its ability to quantify how individual features influence an outcome. In many modern applications, however, datasets contain far more potential predictors than are truly relevant. Identifying a small, meaningful subset of features—sparse modeling—is therefore essential both for interpretability and for avoiding overfitting.
Convex optimization techniques, such as ℓ₁ or ℓ₂ regularization, are commonly used to induce sparsity, but provide less clear insights than non-convex measures, especially when dealing with data that is not uniform in scale. Non-convex methods can provide more precise and more direct insights, but are computationally difficult to solve, especially at scale.
Branch and bound is a promising framework for this task because it can guarantee globally optimal sparse solutions. However, its practical performance is often limited by the size of the search tree, which grows exponentially in the worst case, and the cost of repeatedly solving logistic regression subproblems at each node of the tree.
This project continues the development of a branch and bound solver tailored specifically for sparse logistic regression. Our primary motivation is to close the gap between the theoretical optimality of ℓ₀-based methods and their practical scalability. To do this, we design new algorithms that make far better use of modern hardware. In particular, we introduce parallel mechanisms for the branching procedure and a GPU-accelerated solver for evaluating subproblems.
By leveraging parallel computing and GPU-based optimization, we aim to bring exact sparse logistic regression closer to real-world feasibility on high-dimensional datasets—where interpretability, accuracy, and computational efficiency are all critical.
Research Objective:
The goal of this project is to develop and implement scalable solvers for ℓ₀-constrained logistic regression. Building upon our existing branch and bound framework, our goal is to significantly reduce runtime by designing solvers that leverage hardware capabilities more effectively.
More specifically, we aim to:
- Develop a parallelized branch and bound architecture that distributes branching operations across multiple worker processes with minimal synchronization overhead.
- Develop a GPU-accelerated subproblem solver to dramatically reduce per-node solve time.
- Evaluate performance on real datasets to determine how solver improvements translate into faster global optimization.
Through these efforts, we aim to expand the practical applicability of exact sparse logistic regression to larger datasets and higher-dimensional feature spaces.
Research Methodology:
Parallel Branching
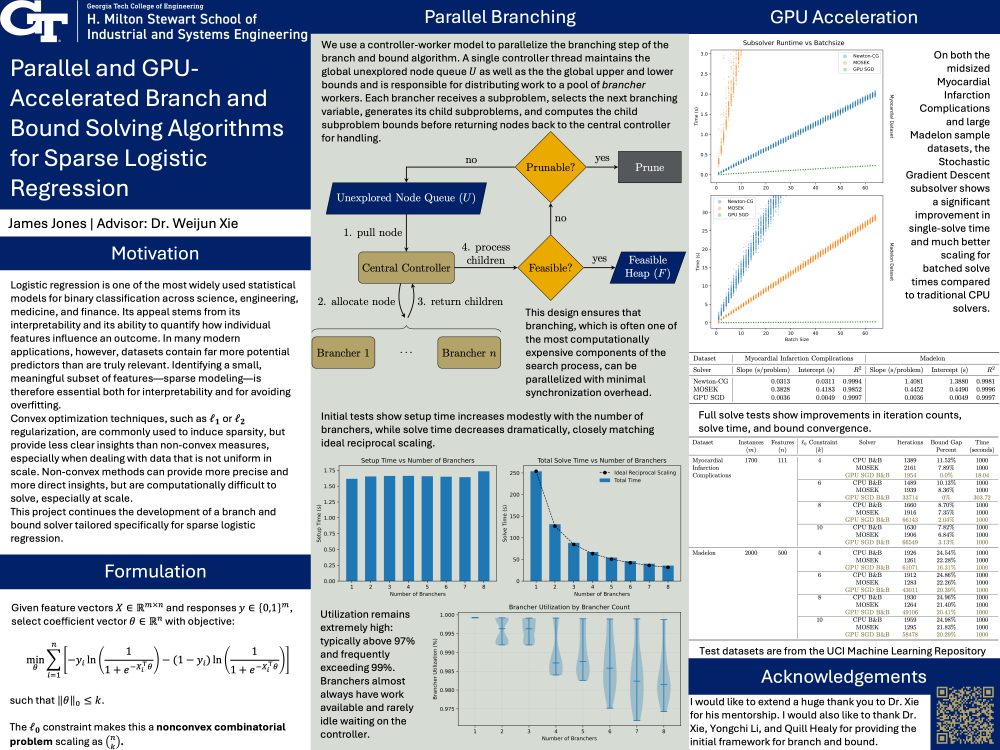
We use a controller-worker model to parallelize the branching step of the branch and bound algorithm. A single controller thread maintains the global unexplored node queue as well as the global upper and lower bounds and is responsible for distributing work to a pool of brancher workers. Each brancher receives a subproblem, selects the next branching variable, generates its child subproblems, and computes the child subproblem bounds before returning nodes back to the central controller for handling.
This design ensures that branching, which is often one of the most computationally expensive components of the search process, can be parallelized with minimal synchronization overhead. The controller performs only lightweight operations—queue management and node dispatch—while all computationally heavy branching and bounding work is offloaded to the workers.
Our implementation uses Python's Multiprocessing Module, with Process objects as branchers and Pipes for communication.
GPU Acceleration
To accelerate the repeated subproblem solves required during branch and bound search, we implemented a stochastic gradient descent (SGD) solver optimized for execution on a GPU. Each subproblem corresponds to fitting a logistic regression model with a restricted feature set determined by the branching decisions made so far. Because these subproblems must be solved thousands of times across the search tree, solver efficiency directly impacts overall performance.
SGD is particularly attractive in this context because its low per-iteration cost and simple update rules map efficiently to GPUs. Our GPU-based solver performs minibatch stochastic gradient updates using CuPy calls to Nvidia's CUDA platform. For each subproblem, the CPU controller assembles the feature-mask for the dataset and transfers it to GPU memory, after which all gradient evaluations, parameter updates, and loss computations are executed on the device. This design minimizes CPU-GPU communication and allows the solver to exploit the high-throughput parallelism of modern GPUs.
Testing Methodology
All tests were conducted using Georgia Tech's AI Makerspace with select datasets from the UCI Machine Learning Repository.
Results:
Parallel Branching
Preliminary tests showed that setup time increases modestly with additional branchers, reflecting the overhead associated with initializing workers. In contrast, total solve time decreases substantially. The observed total speedup closely follows an ideal reciprocal trend, indicating with adequate hardware, further time reductions would be attainable.
Additionally, across all configurations, utilization remains extremely high: typically above 97% and frequently exceeding 99%. This indicates that branchers almost always have work available and rarely idle waiting on the controller.
High utilization across all tested brancher counts suggests that the system is not bottlenecked by load imbalance or by the pace at which the controller supplies work.
GPU Acceleration
Preliminary tests using warm started randomly selected batches from the midsized Myocardial Infarction Complications dataset and large Madelon dataset showed very promising results. We see that not only does SGD achieve more than an order-of-magnitude speedup over CPU-based methods, but it also scales far more efficiently.
These improvements carry through to full problem solving, as for full solves with a 1000 second cutoff, we see improvements in iteration counts, solve time, and bound convergence that are maintained as the problem scales.
Overall, the GPU-accelerated SGD solver provides dramatic reductions in subproblem solve time. When amortized across the full search, these speedups substantially decrease total branch and bound runtime while preserving solution quality. Future enhancements such as selective restarts or multi-start refinement may further mitigate the small number of inaccurate prunes without sacrificing the solver’s performance advantage.
Conclusions and Future Work:
This work demonstrates that significant improvements to convergence rates can be made in branch and bound methods for sparse logistic regression through parallelism and GPU acceleration. Our parallel branching architecture achieves high utilization and near-ideal scaling for moderate numbers of workers, while our GPU-accelerated stochastic gradient solver reduces subproblem runtimes by more than an order of magnitude. Together, these improvements help quicken convergence with minimal loss in pruning accuracy.
The results highlight the potential of combining principled optimization frameworks with modern hardware to solve large-scale nonconvex problems. However, several opportunities remain for further improvement. Future work may include:
- Adaptive strategies to improve the robustness of SGD-based lower bounds.
- Dual-informed bounding techniques to provide tighter relaxations during search.
- Distributed branch-and-bound, extending parallelism across multiple machines.
- Enhanced branching rules to further reduce search tree size.
- Integration into a production-quality solver to support applied scientific and industrial workloads.
Overall, this project demonstrates that exact sparse logistic regression—long viewed as computationally prohibitive—can be made significantly more scalable through thoughtful algorithm–hardware co-design.